Ramas de la física

La mecánica clásica es la rama de la física que estudia las leyes del comportamiento de cuerpos físicos macroscópicos (a diferencia de la mecánica cuántica) en reposo y a velocidades pequeñas comparadas con la velocidad de la luz.

En la mecánica clásica en general se tienen tres aspectos invariantes: el tiempo es absoluto, la naturaleza realiza de forma espontánea la mínima acción y la concepción de un universo determinado.​El primer desarrollo de la mecánica clásica suele denominarse mecánica newtoniana. Consiste en los conceptos físicos basados en los trabajos fundacionales de Sir Isaac Newton, y en los métodos matemáticos inventados por Gottfried Wilhelm Leibniz, Joseph-Louis Lagrange, Leonhard Euler, y otros contemporáneos, en el siglo XVII para describir el movimiento de los cuerpos físicos bajo la influencia de un sistema de fuerzas. Posteriormente, se desarrollaron métodos más abstractos que dieron lugar a las reformulaciones de la mecánica clásica conocidas como mecánica lagrangiana y mecánica hamiltoniana. Estos avances, realizados predominantemente en los siglos XVIII y XIX, van sustancialmente más allá de los trabajos anteriores, sobre todo por su uso de la mecánica analítica. También se utilizan, con algunas modificaciones, en todas las áreas de la física moderna.

La mecánica clásica proporciona resultados extremadamente precisos cuando se estudian objetos grandes que no son extremadamente masivos y velocidades que no se acercan a la velocidad de la luz. Cuando los objetos que se examinan tienen el tamaño del diámetro de un átomo, se hace necesario introducir el otro gran subcampo de la mecánica: la mecánica cuántica. Para describir las velocidades que no son pequeñas en comparación con la velocidad de la luz, se necesita la relatividad especial. En los casos en los que los objetos se vuelven extremadamente masivos, se aplica la relatividad general. Sin embargo, algunas fuentes modernas incluyen la mecánica relativista en la física clásica, que en su opinión representa la mecánica clásica en su forma más desarrollada y precisa.

Existen varias formulaciones diferentes, en mecánica clásica, para describir un mismo fenómeno natural que, independientemente de los aspectos formales y metodológicos que utilizan, llegan a la misma conclusión.

La mecánica vectorial, que deviene directamente de las leyes de Newton, por lo que también se le conoce como «mecánica newtoniana», llega, a partir de las tres ecuaciones formuladas por Newton y mediante el cálculo diferencial e integral, a una muy exacta aproximación de los fenómenos físicos. Es aplicable a cuerpos que se mueven en relación con un observador a velocidades pequeñas comparadas con la de la luz. Fue construida en un principio para una sola partícula moviéndose en un campo gravitatorio. Se basa en el tratamiento de dos magnitudes vectoriales bajo una relación causal: la fuerza y la acción de la fuerza, medida por la variación del momentum (cantidad de movimiento). El análisis y síntesis de fuerzas y momentos constituye el método básico de la mecánica vectorial. Requiere del uso privilegiado de sistemas de referencia inercial.​

La mecánica analítica (analítica en el sentido matemático de la palabra, no en el sentido filosófico) es una formulación matemática abstracta sobre la mecánica; permite desligarse de esos sistemas de referencia privilegiados y tener conceptos más generales al momento de describir un movimiento con el uso del cálculo de variaciones. Sus métodos son poderosos y trascienden de la mecánica a otros campos de la física. Se puede encontrar el germen de la mecánica analítica en la obra de Leibniz, quien propone que para solucionar problemas en mecánica, magnitudes escalares (menos oscuras según Leibniz que la fuerza y el momento de Newton), como energía cinética y el trabajo, son suficientes y menos oscuras que las cantidades vectoriales, como la fuerza y el momento, propuestos por Newton. Existen dos formulaciones equivalentes: la llamada mecánica lagrangiana es una reformulación de la mecánica realizada por Joseph Louis Lagrange que se basa en la ahora llamada ecuación de Euler-Lagrange (ecuaciones diferenciales de segundo orden) y el principio de mínima acción; la otra, llamada mecánica hamiltoniana, es una reformulación más teórica basada en una funcional llamada hamiltoniano realizada por William Hamilton.​ Las mecánicas hamiltoniana y lagrangiana son ejemplos de mecánicas analíticas, donde las magnitudes se relacionan entre sí por ecuaciones diferenciales parciales, que son equivalentes a las ecuaciones de Newton, por ejemplo las ecuaciones canónicas de Hamilton.​

El electromagnetismo es la rama de la física que estudia y unifica los fenómenos eléctricos y magnéticos en una sola teoría. El electromagnetismo describe la interacción de partículas cargadas con campos eléctricos y magnéticos. La interacción electromagnética es una de las cuatro fuerzas fundamentales del universo conocido. Las partículas cargadas interactúan electromagnéticamente mediante el intercambio de fotones.

El electromagnetismo abarca diversos fenómenos del mundo real como por ejemplo la luz. La luz es un campo electromagnético oscilante que se irradia desde partículas cargadas aceleradas. Aparte de la gravedad, la mayoría de las fuerzas en la experiencia cotidiana son consecuencia de electromagnetismo.

Los principios del electromagnetismo encuentran aplicaciones en diversas disciplinas afines, tales como las microondas, antenas, máquinas eléctricas, comunicaciones por satélite, bioelectromagnetismo, plasmas, investigación nuclear, la fibra óptica, la interferencia y la compatibilidad electromagnéticas, la conversión de energía electromecánica, la meteorología por radar, y la observación remota. Los dispositivos electromagnéticos incluyen transformadores, relés, radio/TV, teléfonos, motores eléctricos, líneas de transmisión, guías de onda y láseres.

Los fundamentos de la teoría electromagnética fueron presentados por Michael Faraday y formulados por primera vez de modo completo por James Clerk Maxwell en 1865. La formulación consiste en cuatro ecuaciones diferenciales vectoriales que relacionan el campo eléctrico, el campo magnético y sus respectivas fuentes materiales (corriente eléctrica, polarización eléctrica y polarización magnética), conocidas como ecuaciones de Maxwell, lo que ha sido considerada como la «segunda gran unificación de la física», siendo la primera realizada por Isaac Newton.

La teoría electromagnética se puede dividir en electrostática —el estudio de las interacciones entre cargas en reposo— y la electrodinámica —el estudio de las interacciones entre cargas en movimiento y la radiación—. La teoría clásica del electromagnetismo se basa en la fuerza de Lorentz y en las ecuaciones de Maxwell.

El electromagnetismo es una teoría de campos; es decir, las explicaciones y predicciones que provee se basan en magnitudes físicas vectoriales o tensoriales dependientes de la posición en el espacio y del tiempo. El electromagnetismo describe los fenómenos físicos macroscópicos en los cuales intervienen cargas eléctricas en reposo y en movimiento, usando para ello campos eléctricos y magnéticos y sus efectos sobre las sustancias sólidas, líquidas y gaseosas. Por ser una teoría macroscópica, es decir, aplicable a un número muy grande de partículas y a distancias grandes respecto de las dimensiones de estas, el electromagnetismo no describe los fenómenos atómicos y moleculares. La electrodinámica cuántica proporciona la descripción cuántica de esta interacción, que puede ser unificada con la interacción nuclear débil según el modelo electrodébil.

La teoría de la relatividad incluye tanto a la teoría de la relatividad especial como la de relatividad general, formuladas principalmente por Albert Einstein a principios del siglo XX, que pretendían resolver la incompatibilidad existente entre la mecánica newtoniana y el electromagnetismo. ​La teoría de la relatividad especial, publicada en 1905, trata de la física del movimiento de los cuerpos en ausencia de fuerzas gravitatorias, en el que se hacían compatibles las ecuaciones de Maxwell del electromagnetismo con una reformulación de las leyes del movimiento. En la teoría de la relatividad especial, Einstein, Lorentz y Minkowski, entre otros, unificaron los conceptos de espacio y tiempo, en un ramado tetradimensional al que se le denominó espacio-tiempo. La relatividad especial fue una teoría revolucionaria para su época, con la que el tiempo absoluto de Newton quedó relegado y conceptos como la invariabilidad en la velocidad de la luz, la dilatación del tiempo, la contracción de la longitud y la equivalencia entre masa y energía fueron introducidos. Además, con las formulaciones de la relatividad especial, las leyes de la Física son invariantes en todos los sistemas de referencia inerciales; como consecuencia matemática, se encuentra como límite superior de velocidad a la de la luz y se elimina la causalidad determinista que tenía la física hasta entonces. Hay que indicar que las leyes del movimiento de Newton son un caso particular de esta teoría donde la masa, al viajar a velocidades muy pequeñas, no experimenta variación alguna en longitud ni se transforma en energía y al tiempo se le puede considerar absoluto.

La teoría de la relatividad general, publicada en 1915, es una teoría de la gravedad que reemplaza a la gravedad newtoniana, aunque coincide numéricamente con ella para campos gravitatorios débiles y velocidades «pequeñas». La teoría general se reduce a la teoría especial en presencia de campos gravitatorios. La relatividad general estudia la interacción gravitatoria como una deformación en la geometría del espacio-tiempo. En esta teoría se introducen los conceptos de la curvatura del espacio-tiempo como la causa de la interacción gravitatoria, el principio de equivalencia que dice que para todos los observadores locales inerciales las leyes de la relatividad especial son invariantes y la introducción del movimiento de una partícula por líneas geodésicas. La relatividad general no es la única teoría que describe la atracción gravitatoria, pero es la que más datos relevantes comprobables ha encontrado. Anteriormente, a la interacción gravitatoria se la describía matemáticamente por medio de una distribución de masas, pero en esta teoría no solo la masa percibe esta interacción, sino también la energía, mediante la curvatura del espacio-tiempo y por eso se necesita otro lenguaje matemático para poder describirla, el cálculo tensorial. Muchos fenómenos, como la curvatura de la luz por acción de la gravedad y la desviación en la órbita de Mercurio, son perfectamente predichos por esta formulación. La relatividad general también abrió otro campo de investigación en la física, conocido como cosmología y es ampliamente utilizado en la astrofísica.​

El 7 de marzo de 2010, la Academia Israelí de Ciencias exhibió públicamente los manuscritos originales de Einstein (redactados en 1905). El documento, que contiene 46 páginas de textos y fórmulas matemáticas escritas a mano, fue donado por Einstein a la Universidad Hebrea de Jerusalén en 1925 con motivo de su inauguración.​

Transferencia de calor por convección.

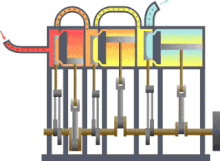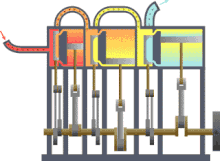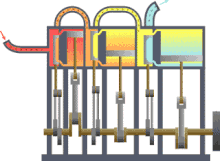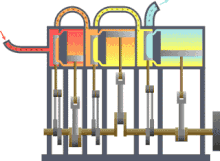
Máquina térmica típica donde se puede observar la entrada desde una fuente de calor (caldera) a la izquierda y la salida a un disipador de calor (condensador) a la derecha. El trabajo se extrae en este caso mediante una serie de pistones.

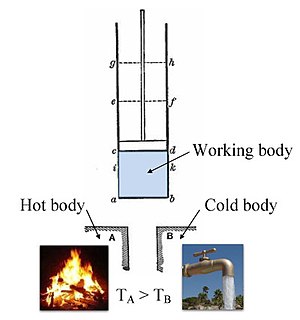
Versión en color anotada de la máquina de calor Carnot original de 1824 que muestra el cuerpo caliente (caldera), el cuerpo de trabajo (sistema, vapor) y el cuerpo frío (agua), las letras etiquetadas de acuerdo con los puntos de parada en el ciclo de Carnot

La termodinámica es la rama de la física que describe los estados de equilibrio termodinámico a nivel macroscópico. El Diccionario de la lengua española de la Real Academia Española, por su parte, define la termodinámica como la rama de la física encargada del estudio de la interacción entre el calor y otras manifestaciones de la energía. Constituye una teoría fenomenológica, a partir de razonamientos deductivos, que estudia sistemas reales, sin modelizar y sigue un método experimental.​ Los estados de equilibrio se estudian y definen por medio de magnitudes extensivas tales como la Energía interna, la entropía, el volumen o la composición molar del sistema,​ o por medio de magnitudes no-extensivas derivadas de las anteriores como la temperatura, presión y el potencial químico; otras magnitudes, tales como la imanación, la fuerza electromotriz y las asociadas con la mecánica de los medios continuos en general también se pueden tratar por medio de la termodinámica.​

La termodinámica trata los procesos de transferencia de calor, que es una de las formas de energía y cómo se puede realizar un trabajo con ella. En esta área se describe cómo la materia en cualquiera de sus fases (sólido, líquido, gaseoso) va transformándose. Desde un punto de vista macroscópico de la materia, se estudia cómo esta reacciona a cambios en su volumen, presión y temperatura, entre otras magnitudes. La termodinámica se basa en cuatro[[principios de la termodinámica] los cuales son]]: el equilibrio termodinámico (o principio cero), el principio de conservación de la energía (primer principio), el aumento temporal de la entropía (segundo principio) y la imposibilidad del cero absoluto (tercer principio).​

Una consecuencia de la termodinámica es lo que hoy se conoce como física estadística. Esta rama estudia, al igual que la termodinámica, los procesos de transferencia de calor, pero, al contrario a la anterior, desde un punto de vista molecular. La materia, como se conoce, está compuesta por moléculas, y el conocer el comportamiento de una sola de sus moléculas nos lleva a medidas erróneas. Por eso se debe tratar como un conjunto de elementos caóticos o aleatorios y se utiliza el lenguaje estadístico y consideraciones mecánicas para describir comportamientos macroscópicos de este conjunto molecular microscópico.​

La termodinámica ofrece un aparato formal aplicable únicamente a estados de equilibrio,​ definidos como aquel estado hacia «el que todo sistema tiende a evolucionar y caracterizado porque en el mismo todas las propiedades del sistema quedan determinadas por factores intrínsecos y no por influencias externas previamente aplicadas». ​Tales estados terminales de equilibrio son, por definición, independientes del tiempo, y todo el aparato formal de la termodinámica —todas las leyes y variables termodinámicas— se definen de tal modo que se podría decir que un sistema está en equilibrio si sus propiedades se pueden describir consistentemente empleando la teoría termodinámica. Los estados de equilibrio son necesariamente coherentes con los contornos del sistema y las restricciones a las que esté sometido. Por medio de los cambios producidos en estas restricciones (esto es, al retirar limitaciones tales como impedir la expansión del volumen del sistema, impedir el flujo de calor, etc.), el sistema tenderá a evolucionar de un estado de equilibrio a otro; comparando ambos estados de equilibrio, la termodinámica permite estudiar los procesos de intercambio de masa y energía térmica entre sistemas térmicos diferentes.

Como ciencia fenomenológica, la termodinámica no se ocupa de ofrecer una interpretación física de sus magnitudes. La primera de ellas, la energía interna, se acepta como una manifestación macroscópica de las leyes de conservación de la energía a nivel microscópico, que permite caracterizar el estado energético del sistema macroscópico (macroestado).​ El punto de partida para la mayor parte de las consideraciones termodinámicas son los que postulan que la energía se puede intercambiar entre sistemas en forma de calor o trabajo, y que solo se puede hacer de una determinada manera. También se introduce una magnitud llamada entropía,⁷⁵​ que se define como aquella función extensiva de la energía interna, el volumen y la composición molar que toma valores máximos en equilibrio: el principio de maximización de la entropía define el sentido en el que el sistema evoluciona de un estado de equilibrio a otro.​ Es la física estadística, íntimamente relacionada con la termodinámica, la que ofrece una interpretación física de ambas magnitudes: la energía interna se identifica con la suma de las energías individuales de los átomos y moléculas del sistema, y la entropía mide el grado de orden y el estado dinámico de los sistemas, y tiene una conexión muy fuerte con la teoría de información.​ En la termodinámica se estudian y clasifican las interacciones entre diversos sistemas, lo que lleva a definir conceptos como sistema termodinámico y su contorno. Un sistema termodinámico se caracteriza por sus propiedades, relacionadas entre sí mediante las ecuaciones de estado. Estas se pueden combinar para expresar la energía interna y los potenciales termodinámicos, útiles para determinar las condiciones de equilibrio entre sistemas y los procesos espontáneos.

Con estas herramientas, la termodinámica describe cómo los sistemas reaccionan a los cambios en su entorno. Esto se puede aplicar a una amplia variedad de ramas de la ciencia y de la ingeniería, tales como motores, cambios de fase, reacciones químicas, fenómenos de transporte e incluso agujeros negros.

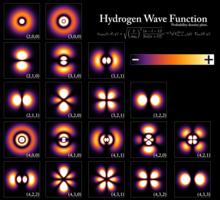
Funciones de onda del electrón en un átomo de hidrógeno a diferentes niveles de energía. La mecánica cuántica no puede predecir la ubicación exacta de una partícula en el espacio, solo la probabilidad de encontrarla en diferentes lugares. Las áreas más brillantes representan una mayor probabilidad de encontrar el electrón.

Esquema de una función de onda monoelectrónica u orbital en tres dimensiones.

Esquema de un orbital en dos dimensiones.

La mecánica cuántica es la rama de la física que estudia la naturaleza a escalas espaciales pequeñas. Los sistemas atómicos y subatómicos, sus interacciones con la radiación electromagnética y otras fuerzas, en términos de cantidades observables. Se basa en la observación de que todas las formas de energía se liberan en unidades discretas o paquetes llamados cuantos. Estos cuantos tienen la característica de pertenecer todos a un grupo específico de bosones, estando cada uno ligado a una interacción fundamental. (Ej: el fotón pertenece a la electromagnética). Sorprendentemente, la teoría cuántica solo permite normalmente cálculos probabilísticos o estadísticos de las características observadas de las partículas elementales, entendidos en términos de funciones de onda. La ecuación de Schrödinger desempeña el papel en la mecánica cuántica que las leyes de Newton y la conservación de la energía hacen en la mecánica clásica. Es decir, la predicción del comportamiento futuro de un sistema dinámico y es una ecuación de onda en términos de una función de onda la que predice analíticamente la probabilidad precisa de los eventos o resultados.

En teorías anteriores de la física clásica, la energía era tratada únicamente como un fenómeno continuo, en tanto que la materia se supone que ocupa una región muy concreta del espacio y que se mueve de manera continua. Según la teoría cuántica, la energía se emite y se absorbe en cantidades discretas y minúsculas. Un paquete individual de energía, llamado cuanto, en algunas situaciones se comporta como una partícula de materia. Por otro lado, se encontró que las partículas exponen algunas propiedades ondulatorias cuando están en movimiento y ya no son vistas como localizadas en una región determinada, sino más bien extendidas en cierta medida. La luz u otra radiación emitida o absorbida por un átomo solo tiene ciertas frecuencias (o longitudes de onda), como puede verse en la línea del espectro asociado al elemento químico representado por tal átomo. La teoría cuántica demuestra que tales frecuencias corresponden a niveles definidos de los cuantos de luz, o fotones, y es el resultado del hecho de que los electrones del átomo solo pueden tener ciertos valores de energía permitidos. Cuando un electrón pasa de un nivel permitido a otro, una cantidad de energía es emitida o absorbida, cuya frecuencia es directamente proporcional a la diferencia de energía entre los dos niveles.

La mecánica cuántica surge tímidamente en los inicios del siglo xx dentro de las tradiciones más profundas de la física para dar una solución a problemas para los que las teorías conocidas hasta el momento habían agotado su capacidad de explicar, como la llamada catástrofe ultravioleta en la radiación de cuerpo negro predicha por la física estadística clásica y la inestabilidad de los átomos en el modelo atómico de Rutherford. La primera propuesta de un principio propiamente cuántico se debe a Max Planck en 1900, para resolver el problema de la radiación de cuerpo negro, que fue duramente cuestionado, hasta que Albert Einstein lo convierte en el principio que exitosamente pueda explicar el efecto fotoeléctrico. Las primeras formulaciones matemáticas completas de la mecánica cuántica no se alcanzan hasta mediados de la década de 1920, sin que hasta el día de hoy se tenga una interpretación coherente de la teoría, en particular del problema de la medición.

El formalismo de la mecánica cuántica se desarrolló durante la década de 1920. En 1924, Louis de Broglie propuso que, al igual que las ondas de luz presentan propiedades de partículas, como ocurre en el efecto fotoeléctrico, las partículas, también presentan propiedades ondulatorias. Dos formulaciones diferentes de la mecánica cuántica se presentaron después de la sugerencia de Broglie. En 1926, la mecánica ondulatoria de Erwin Schrödinger implica la utilización de una entidad matemática, la función de onda, que está relacionada con la probabilidad de encontrar una partícula en un punto dado en el espacio. En 1925, la mecánica matricial de Werner Heisenberg no hace mención alguna de las funciones de onda o conceptos similares, pero ha demostrado ser matemáticamente equivalente a la teoría de Schrödinger. Un descubrimiento importante de la teoría cuántica es el principio de incertidumbre, enunciado por Heisenberg en 1927, que pone un límite teórico absoluto en la precisión de ciertas mediciones. Como resultado de ello, la asunción clásica de los científicos de que el estado físico de un sistema podría medirse exactamente y utilizarse para predecir los estados futuros tuvo que ser abandonada. Esto supuso una revolución filosófica y dio pie a numerosas discusiones entre los más grandes físicos de la época.

La mecánica cuántica propiamente dicha no incorpora a la relatividad en su formulación matemática. La parte de la mecánica cuántica que incorpora elementos relativistas de manera formal para abordar diversos problemas se conoce como mecánica cuántica relativista o ya, en forma más correcta y acabada, teoría cuántica de campos (que incluye a su vez a la electrodinámica cuántica, cromodinámica cuántica y teoría electrodébil dentro del modelo estándar) y más generalmente, la teoría cuántica de campos en espacio-tiempo curvo. La única interacción elemental que no se ha podido cuantizar hasta el momento ha sido la interacción gravitatoria. Este problema constituye entonces uno de los mayores desafíos de la física del siglo xxi. La mecánica cuántica se combinó con la teoría de la relatividad en la formulación de Paul Dirac de 1928, lo que, además, predijo la existencia de antipartículas. Otros desarrollos de la teoría incluyen la estadística cuántica, presentada en una forma por Einstein y Bose (la estadística de Bose-Einstein) y en otra forma por Dirac y Enrico Fermi (la estadística de Fermi-Dirac); la electrodinámica cuántica, interesada en la interacción entre partículas cargadas y los campos electromagnéticos, su generalización, la teoría cuántica de campos y la electrónica cuántica.

La mecánica cuántica proporciona el fundamento de la fenomenología del átomo, de su núcleo y de las partículas elementales (lo cual requiere necesariamente el enfoque relativista). También su impacto en teoría de la información, criptografía y química ha sido decisivo entre esta misma.

Fuente: Wikipedia